概述

本文主要通过介绍正则表达式中的一些进阶内容，让读者了解正则表达式在日常使用中用到的比较少但是又比较重要的一部分内容，从而让大家对正则表达式有一个更加深刻的认识。

本文的主要内容为：

• 正则表达式回溯法原理
• 正则表达式操作符优先级

本文不介绍相关正则表达式的基本用法，如果对正则表达式的基本使用方法还不了解的同学，可以阅读我的上一篇博客——正则表达式语法入门。

回溯法原理

回溯是影响正则表达式效率的一个非常重要的原因，我们在进行正则表达式匹配时，一定要尽可能的避免回溯。

很多人可能只是对听说过“回溯法”，并不了解其中具体内容和原理，接下来就先让我们看下什么是回溯法。

回溯法的定义

回溯法就是指正则表达式从头开始依次进行匹配，如果匹配到某个特定的情况下时，发现无法继续进行匹配，需要回退到之前匹配的结果，选择另一个分支继续进行匹配中的现象。这个描述可能有点抽象，我们举一个简单的例子，让大家能够更加明确的理解回溯法：

const reg = /ab{1,3}c/;

const str = 'abbc';

// 第1步：匹配/a/，得到'a'
// 第2步：匹配/ab{1}/，得到'ab'
// 第3步：匹配/ab{2}/，得到'abb'
// 第4步：匹配/ab{3}/，匹配失败，需要进行回溯
// 第5步：回溯到/ab{2}/,继续匹配/ab{2}c/，得到'abbc'
// 第6步：正则表达式匹配完成，得到'abbc'

如果我们把正则表达式的各个分支都整理成一棵树的话，正则表达式的匹配其实就是一个深度优先搜索算法。而回溯其实就是在进行深度优先匹配失败后的后退正常操作逻辑。

如果退回到了根节点仍然无法匹配的话，就会将index向后移动一位，重新构建匹配数。即/bc/在'abc'时，由于第一个字符'a'无法匹配，则移动到'b'开始匹配。

回溯法产生场景

理解了回溯法和回溯操作，接下来我们来看下什么场景下会出现回溯。出现回溯的场景主要有以下几种：

1. 贪婪量词（贪婪匹配）
2. 惰性量词（非贪婪匹配）
3. 分支结构（分支匹配）

接下来，让我们一个一个来看下这些场景是如何出现回溯的。

贪婪量词（贪婪匹配）

const reg = /ab{1,3}c/;

const str = 'abbc';

// 第1步：匹配/a/，得到'a'
// 第2步：匹配/ab{1}/，得到'ab'
// 第3步：匹配/ab{2}/，得到'abb'
// 第4步：匹配/ab{3}/，匹配失败，需要进行回溯
// 第5步：回溯到/ab{2}/,继续匹配/ab{2}c/，得到'abbc'
// 第6步：正则表达式匹配完成，得到'abbc'

最开始的例子其实就是一个贪婪匹配的示例，通过尽可能多的匹配b从而导致了回溯。

惰性量词（非贪婪匹配）

const reg = /ab{1,3}?c/;

const str = 'abbc';

// 第1步：匹配/a/，得到'a'
// 第2步：匹配/ab{1}/，得到'ab'
// 第3步：匹配/ab{1}c/，匹配失败，需要进行回溯
// 第4步：回溯到/ab{1}/，继续匹配/ab{2}/，得到'abb'
// 第5步：匹配/ab{2}c/，得到'abbc'
// 第6步：正则表达式匹配完成，得到'abbc'

与贪婪匹配类似，非贪婪匹配虽然每次都是去最小匹配数目，但是也会出现回溯的情况。

分支结构（分支匹配）

const reg = /(ab|abc)d/;

const str = 'abcd';

// 第1步：匹配/ab/，得到'ab'
// 第2步：匹配/abd/，匹配失败，需要进行回溯
// 第3步：回溯到//，继续匹配/abc/，得到'abc'
// 第4步：匹配/abcd/，得到'abcd'
// 第5步：正则表达式匹配完成，得到'abcd'

通过上面的示例我们可以看到，分支结构在出现两个分支情况类似的时候，也会出现回溯的情况，在这种情况下，如果一个分支无法匹配，则会回到这个分支的最初情况来重新进行匹配。

正则表达式操作符优先级

看完了回溯法，下面我们来了解下关于正则表达式操作符的优先级。

我们直接看结论，然后再根据结论来给大家提供示例进行理解。

操作符描述	操作符	优先级
转移符	\|1
小括号和中括号	(…)、(?:…)、(?=…)、(?!…)、[…]	2
量词限定符	{m}、{m,n}、{m,}、?、*、+	3
位置和序列	^、$、\元字符、一般字符	4
管道符	|	5

通过操作符的优先级，我们能够知道如何来读一个正则表达式。以下面这个正则表达式为例，我们来介绍一下按照优先级进行分析的方法：

const reg = /ab?(c|de*)+|fg/;

// 第一步，根据优先级先考虑(c|de*)+，再根据优先级拆分得到c de*，即匹配c或者de*（注意，位置和序列的优先级高于管道符|，所以是c或de*而不是c或d和e*）
// 第二步，得到ab?，根据优先级拆分得到a和b?
// 第三步，得到fg，这个内容和第一步+第二步的结果为或的关系

最终，我们得到的效果如下：

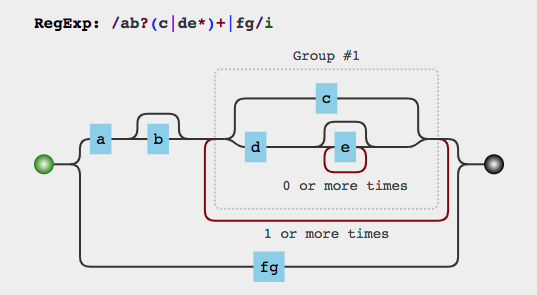
通过这个图，大家就能够理解我们的分析思路：先找括号，括号中的一定为一个整体（转移符只做转义，不分割正则，因此可以认为第一优先级其实是括号），没有括号后再从左到右按照优先级进行分析。量词限定符则看做是正则的一个整体。

注：如果大家需要话类似的正则表达式流程图，可以使用此网站。

根据上面的优先级，我们就能够避免在正则表达式的理解中出现归类错误的情况。

总结

本文通过介绍在正则表达式中容易被忽略的两个内容：回溯法和操作优先级，让大家能够在进行正则的阅读和书写过程中避免踩到相关的坑。

参考内容

1. 《JavaScript正则表达式迷你书》——老姚 V1.1
2. 《JavaScript权威指南》